-
Addition, multiplication, and their combinations
CIS-77 Home http://www.c-jump.com/CIS77/CIS77syllabus.htm
|
|
Wires conduct electricity. When there is a potential difference, it causes electric difference and flow of electric current.
High or low amount of electric current can represent a two types of signals...
...so one wire can represent a logical zero or a logical one.
Eight wires can represent 256 unique combinations of 1s and 0s.
In general, k wires can represent 2k different combinations of 1s and 0s.
A combination of bit patterns is a code that represents a data value.
Values can be encoded in a computer as bit patterns.
Operations on values recognize data types, in conjunction with the encoded information.
This means that ISA(*) operations are constrained to operate only on particular data types.
A data type presumes knowledge about data size, set of operations, and internal order of encoding of the actual 1s and 0s.
For example,
positive and negative integers
floating point numbers, such as 3.14
ASCII codes that represent printable characters
____________
(*) ISA stands for Instruction Set Architecture.
Typical usage as counters.
Identification of memory locations.
With k bits we can represent 2k unique numbers.
We also need to be able to represent negative quantities.
In arithmetics, a minus sign is used as a prefix in notation of negative numbers.
In a combination of bits, a leftmost bit could indicate the sign.
Therefore,
one half of integer numbers could represent positive numbers,
another half - negative numbers.
Decision to make: what codes should we assign to what values?
Positive numbers and zero can be presented in a straightforward positional scheme.
For example, largest positive member of a 5-bit pattern is 01111, or decimal 15.
|
|
|
|
|
|
|
|
Addition rules of two 2's complement integers are quite simple:
If two numbers with opposite signs are added, the result is zero.
Also, representation of value+1 equals to the representation of value plus representation of 1 .
Addition of positive numbers mirrors addition of decimal numbers, that is,
if a column generates a carry, it is added to the column immediately to the left.
If overflow occurs, last carry out is ignored (thrown away.)
If number is negative,
find 2's complement of the positive number of the same magnitude.
For example, to find decimal value of 8-bit number 11000111,
Calculate its 2's complement: 00111001.
Then use the formula:
0*27 + 0*26 + 1*25 + 1*24 + 1*23 + 0*22 + 0*21 + 1*20 = 32+16+8+1 = 57
Finally, add the minus sign: the answer is -57.
Consider a decimal integer 105, which we would like to convert to a signed 8-bit quantity:
position: 76543210
value: ????????
105 a positive, odd number.
Our task is to find values of bits a7 through a0 as follows:
105 = a7*27 + a6*26 + a5*25 + a4*24 + a3*23 + a2*22 + a1*21 + a0*20
a7 is zero, because 105 is positive:
position: 76543210
value: 0???????
a0 is one, because 105 is odd:
position: 76543210
value: 0??????1
Subtracting one from 105 yields 104:
104 = a6*26 + a5*25 + a4*24 + a3*23 + a2*22 + a1*21
Dividing both sides of the equation by 2 yields
52 = a6*25 + a5*24 + a4*23 + a3*22 + a2*21 + a1*20
Since 52 is even, so a1 equals to zero:
position: 76543210
value: 0?????01
Next, we can iterate back to
step 5, if the number is odd, and subtract again last digit, or
step 6, if the number is even, and divide both sides of the equation by two.
In our example dividing both sides by 2 yields
26 = a6*24 + a5*23 + a4*22 + a3*21 + a2*20, therefore a2 = 0:
position: 76543210
value: 0????001
Dividing both sides by 2 yields
13 = a6*23 + a5*22 + a4*21 + a3*20, therefore a3 = 1:
position: 76543210
value: 0???1001
Subtracting one from both sides yields
12 = a6*23 + a5*22 + a4*21
Dividing both sides by 2 yields
6 = a6*22 + a5*21 + a4*20, therefore a4 = 0:
position: 76543210
value: 0??01001
Dividing both sides by 2 yields
3 = a6*21 + a5*20, therefore a5 = 1:
position: 76543210
value: 0?101001
And, finally,
1 = a6*20, therefore a6 = 1:
position: 76543210
value: 01101001
Conversion to 2's complement integers can be summarized by the following steps:
If number is even, the rightmost bit is zero.
If number is odd, the rightmost bit is one.
Subtract zero or one.
Divide both sides by 2.
Repeat.
The series of iterations produce a sequence of bit patterns from right to left.
If original decimal number is negative,
Follow steps 1-5 from above.
Append leading zero bit to the result.
Convert the result to 2's complement representation by taking complement and adding one.
More examples here:
Conversion of positive to negative and vice versa is a negation operation.
This is a two-step operation:
take complement
add one
Note: ignore (throw away) carry out of the leftmost bit.
Difference
A - B
is calculated as addition with the negative number, that is,
A + (-B)
The addition A + (-B) mirrors addition of decimal numbers, that is,
if a column generates a carry, it is added to the column immediately to the left.
Moving 2's complement integers between data types of different sizes is illegal without the sign extension operation.
When necessary, you must sign-extend integer to convert signed value to a larger size.
Sign-extending means copying the sign bit of the unextended value to all bits on the left side of the larger-size value.
For example, 8-bit encoding of decimal number -56 can be sign-extended as follows:
11001000 <- 8-bit value of -56
11111111 11001000 <- extended to 16-bit value
11111111 11111111 11111111 11001000 <- extended 32-bit value
The same way as leading zeroes do not affect values of a positive numbers, leading 1s do not affect values of a negative numbers.
Sign-extend operation is often abbreviated SEXT.
SEXT widens the data while maintaining its sign and value.
Sign extending operation efficiently converts positive values as well, provided the sign bit is zero:
01001000 <- 8-bit value of 72
00000000 01001000 <- extended to 16-bit value
00000000 00000000 00000000 01001000 <- extended 32-bit value
Note: it is programmer's responsibility to keep track of which values are signed or unsigned, and treat them accordingly.
Arithmetic operations have a potential to run into a condition known as overflow.
Overflow occurs with respect to the size of the data type that must accommodate the result.
Overflow indicates that the result was too large or too small to fit in the original data type.
For example, when the sum of two positive 8-bit numbers exceeds 127, we have an overflow.
Similarly, if sum of two negative 8-bit numbers is less than or equal to -128, we have an overflow.
When two signed (2's complement) numbers are added, overflow is detected if:
both operands are positive and the result is negative, or
both operands are negative and the result is positive.
When two unsigned numbers are added, overflow occurrs if there is a carry out of the leftmost bit.
Addition, negation, and subtraction are arithmetic operations.
Another class of operations is defined as logical operations.
Logical meaning of 1 is true;
Logical meaning of 0 is false.
|
|
OR is another binary logical function with two operands:
| A | B | OR(A,B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
|
|
|
|
Logical operations can be used to apply masks to bit patterns.
The masks are used when there is a need to set some bit positions to 1 or to 0.
Only specified bit positions are updated, while other bits are ignored...
...hence the technical term, bit mask.
A typical use of masks is:
Use (X OR 1) to set X bit to 1
Use (X OR 0) to leave X bit unchanged
Use (X AND 0) to set X bit to 0
Use (X AND 1) to leave X bit unchanged
Self-study: please read pages textbook 37-40, floating point data type.
See also: C++ Floating-point variables
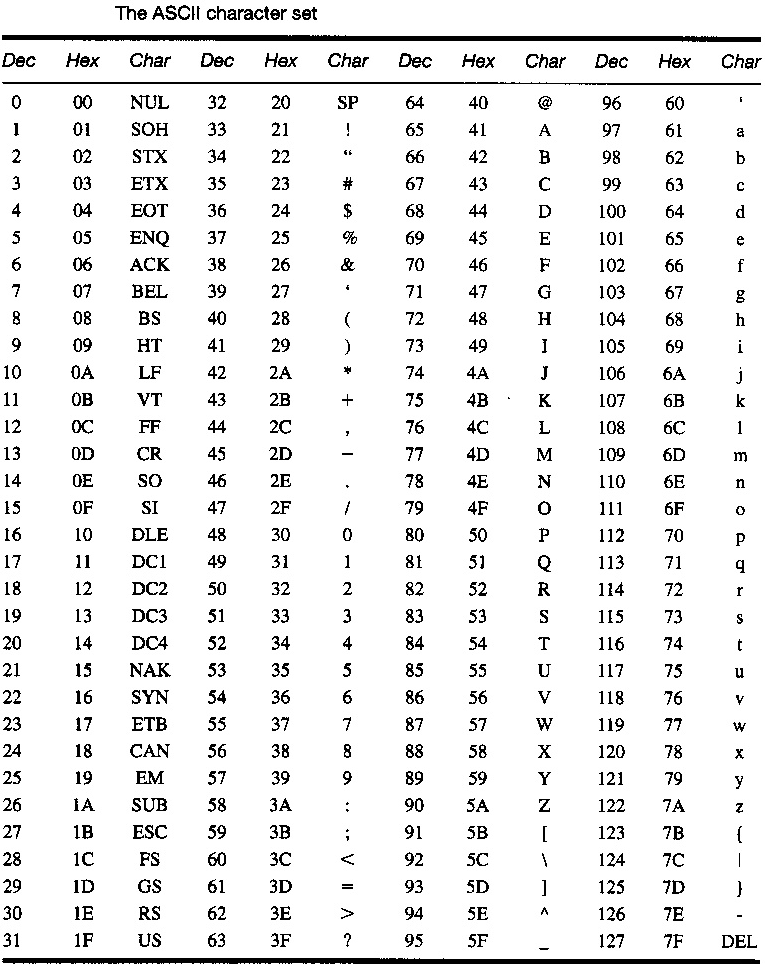
ASCII stands for American Standard Code for Information Interchange.
Used for transferring codes of characters between CPU and I/O devices.
Supports 8-bit representation of character encodings.
|
|