3-221
INSTRUCTION SET REFERENCE
FPATANPartial Arctangent
Description
This instruction computes the arctangent of the source operand in register ST(1) divided by the
source operand in register ST(0), stores the result in ST(1), and pops the FPU register stack. The
result in register ST(0) has the same sign as the source operand ST(1) and a magnitude less than
+?
.
The FPATAN instruction returns the angle between the X axis and the line from the origin to the
point (X,Y), where Y (the ordinate) is ST(1) and X (the abscissa) is ST(0). The angle depends
on the sign of X and Y independently, not just on the sign of the ratio Y/X. This is because a
point (
?
X,Y) is in the second quadrant, resulting in an angle between
?
/2 and
?
, while a point
(X,
?
Y) is in the fourth quadrant, resulting in an angle between 0 and
??
/2. A point (
?
X,
?
Y) is
in the third quadrant, giving an angle between
??
/2 and
??
.
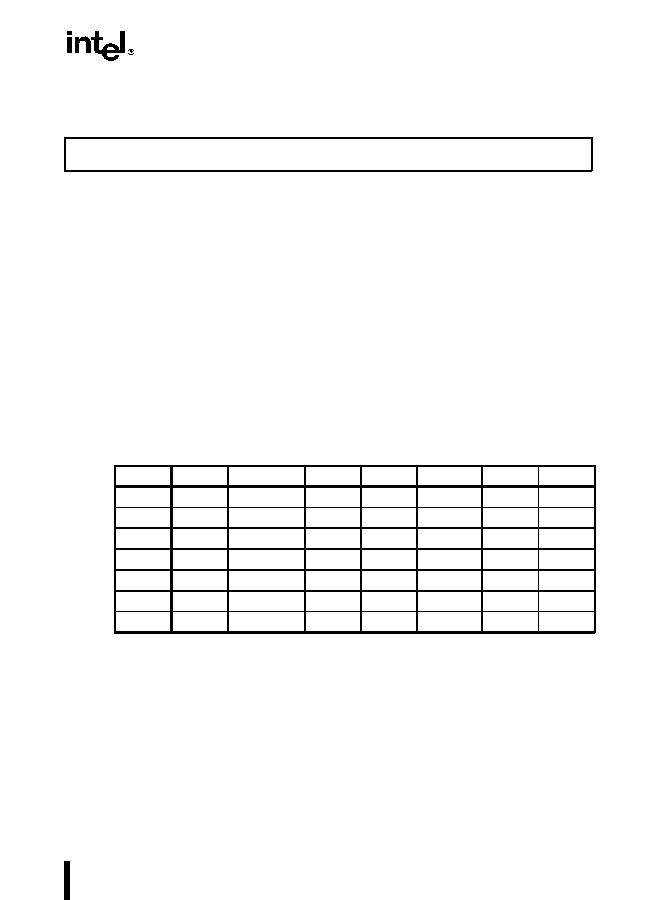
The following table shows the results obtained when computing the arctangent of various
classes of numbers, assuming that underflow does not occur.
NOTES:
FMeans finite-real number.
*Table 7-21 in Chapter 7, Floating-Point Unit of the Intel Architecture Software Developers Manual, Vol-
ume 1, specifies that the ratios 0/0 and
?
/
?
generate the floating-point invalid arithmetic-operation excep-
tion and, if this exception is masked, the real indefinite value is returned. With the FPATAN instruction, the
0/0 or
?
/
?
value is actually not calculated using division. Instead, the arctangent of the two variables is
derived from a common mathematical formulation that is generalized to allow complex numbers as argu-
ments. In this complex variable formulation, arctangent(0,0) etc. has well defined values. These values
are needed to develop a library to compute transcendental functions with complex arguments, based on
the FPU functions that only allow real numbers as arguments.
There is no restriction on the range of source operands that FPATAN can accept.
OpcodeInstructionDescription
D9 F3FPATAN
Replace ST(1) with arctan(ST(1)
/
ST(0)) and pop the register stack
ST(0)
??
?
F
?
0
+
0
+
F
+
?
NaN
???
3
?/
4
*
??
/2
??
/2
??
/2
??
/2
??
/4
*
NaN
ST(1)
?
F
????
to
??/
2
??
/2
??
/2
??/
2
to
?
0-0NaN
?
0
??
??
??
*
?
0
*
?
0
?
0NaN
+0
+
?
+
?
+
?
*
+0
*
+0
+0NaN
+
F
+
?
+
?
to
+
?/
2+
?/
2+
?/
2
+
?/
2
to +
0+0NaN
+
?
+3
?/
4
*
+
?/
2
+
?/
2+
?/
2+
?/
2
+
?
/4
*
NaN
NaNNaN
NaN
NaNNaNNaNNaNNaN