-
Trigonometry == relationships involving lengths and angles of triangles
-
Trigonometry works on a flat, two-dimensional surface (a plane)
-
Our application of trigonometry will be focusing on analyzing angles between vectors in space

Course list http://www.c-jump.com/bcc/
|

|
|
|




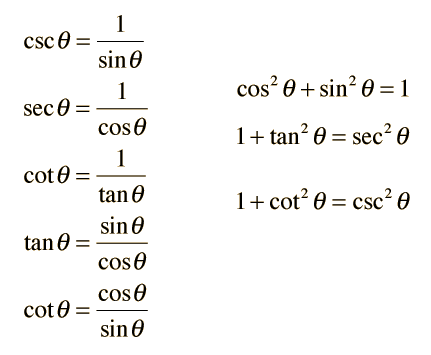

Trigonometrical functions are defined by the relationships of the sides of a triangle
Commonly used: sine, cosine, tangent and cotangent
Sine and cosine produce the same values by adding/subtractng PI/2 (90 degrees)
Less used: secant, cosecant, cotangent


 (From http://upload.wikimedia.org/wikipedia/commons/2/23/Trigonometry_Formulas.png)
(From http://upload.wikimedia.org/wikipedia/commons/2/23/Trigonometry_Formulas.png)
More: http://www.alef.net/ALEFThings/ReferenceCards/ALEFReferenceCards-Trigonometry%20-%20Side%202.Jpg