Vectors

Course list http://www.c-jump.com/bcc/

Vectors

Points
Vectors
Vector magnitude (length)
Vector multiplication by scalar
Sum of vectors
Inverse
Point+vector addition
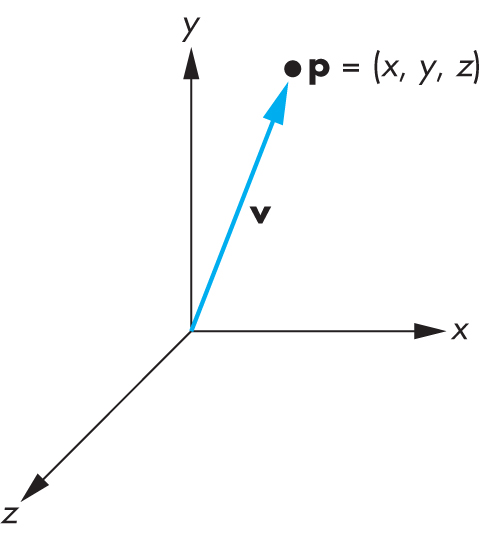
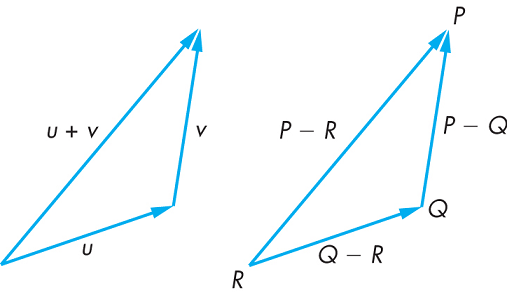
Head-to-tail rule
Dot product
Dot product, cont.
Cross product
Cross product, cont.
Normal to the plane
Using dot product to find a projection vector

1. Points

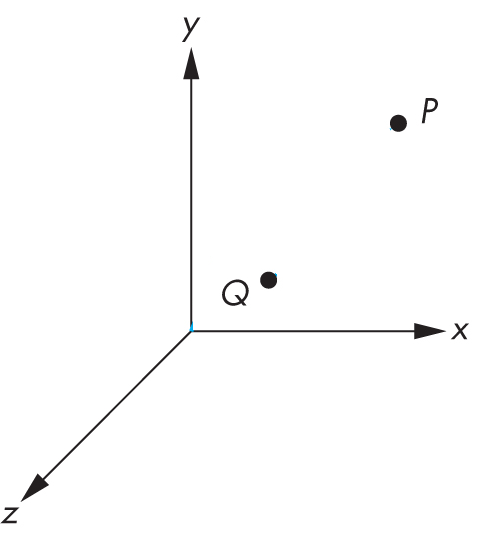
Points in 3D space, such as P and Q
- specify location in space
- don't have size or shape

points in 3D

2. Vectors

We need an additional type -- vector, which provides direction.
We can combine points and vectors to organize our geometry and specify its orientation in 3D space.

vectors in 3D

3. Vector magnitude (length)

Vectors also have length, or magnitude:

coordinates vector point

4. Vector multiplication by scalar

We define scalar is a real number, such as 2, 0.033, 10.5, and so on.
Vector's length can be altered by scalar multiplication, for example,
- B = 2A

vector multiplication by scalar

5. Sum of vectors

Two vectors A and C can be combined by connecting head of vector A with tail of vector C, resulting in vector D which is called the sum of two vectors:
- D = A + C

sum of vectors

6. Inverse

Vector E is an inverse of A when
- E = -A
This is important, because it allows to construct expressions such as
- A + 2B -3C

inverse vector

7. Point+vector addition

Point+vector addition allows to move from one point to another
- P = Q + v
At the same time,
- v = P - Q
The last equation defines point-point subtraction, which yields a vector.

point vector addition

8. Head-to-tail rule

The head-to-tail rule gives us a convenient way of visualizing vector+vector addition. It can be applied to both vector+vector as well as individual points:
- u + v
- (P - Q) + (Q - R) = P - R

head to tail rule

9. Dot product

Dot product is defined as the cosine of the angle a between two vectors u and v, multiplied by the lengths of both vectors:
- u·v = |u||v|cos(a)
  (Geometric definition)
- u·v = u.x*v.x + u.y*v.y + u.z*v.z
  (Algebraic definition -- used more often)
Thus, dot product is a scalar value.
The order of operands is not important:
- u·v = v·u

dot product

10. Dot product, cont.

The following properties of dot product make it especially important for us:
1. If u and v are of unit length (the length of 1), then u·v is the cos(a)
2. The dot product is used extensively during diffuse lighting calculations. It is taken between a surface normal and the vector pointing toward a light source. When the angle is zero, the light intensity is at its maximum.
3. The magnitude (length) of a vector is usually measured as
  - |v| = sqrt( v·v )
4. If
  - u·v = 0
  then u and v are orthogonal (positioned at 90 degree angle)

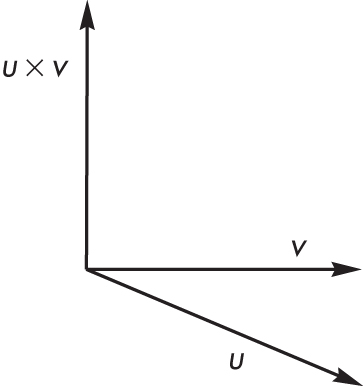
11. Cross product

The cross product between two vectors u and v is a vector which is perpendicular to both u and v:
- u×v = |u||v|sin(a) * n
where n is a unit vector perpendicular to both u and v.
If both u and v are of unit length (length of 1), then u×v will be also of unit length.

u×v can also be calculated using coordinates:

          |  u.y * v.z - u.z * v.y  |
    u×v = |  u.z * v.x - u.x * v.z  |
          |  u.x * v.y - u.y * v.x  |

If u and v are normalized, then
- u×v = sin(a) * n

cross product

12. Cross product, cont.

Note: unlike the dot product, the order of vectors is important: if the order is reversed, the reseulting vector is pointing in the opposite direction:
- u×v = N
- v×u = -N
The cross product gives a consistent orientation: given the usual x and y axis in space, the u×v is pointing in the direction of the positive z axis.
The cross product has numerous purposes, including finding normals and constructing translation matrices.

13. Normal to the plane

If you normalize the cross product (make it of unit length), then you get the normal to the plane.
Unit vector n can be obtained as
- n = N / |N|

plane normal

14. Using dot product to find a projection vector

To find vector p that is a projection of vector u onto v,
1. First find projection length:
  - projection length = |u|cos(a) = (u·v)/|v|
2. To find projection vector, multiply projection length by v's unit vector v / |v|:
  - p = (u·v)/|v| * v/|v| = (u·v)/|v|² * v

dot product