11. Cross product

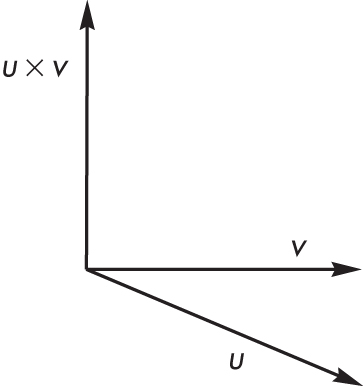
The cross product between two vectors u and v is a vector which is perpendicular to both u and v:

• u×v = |u||v|sin(a) * n

where n is a unit vector perpendicular to both u and v.

If both u and v are of unit length (length of 1), then u×v will be also of unit length.

u×v can also be calculated using coordinates:

          |  u.y * v.z - u.z * v.y  |
    u×v = |  u.z * v.x - u.x * v.z  |
          |  u.x * v.y - u.y * v.x  |

If u and v are normalized, then

• u×v = sin(a) * n