7-5
FLOATING-POINT UNIT
Representing numbers in normalized form maximizes the number of significant digits that can
be accommodated in a significand of a given width. To summarize, a normalized real number
consists of a normalized significand that represents a real number between 1 and 2 and an expo-
nent that specifies the numbers binary point.
7.2.2.2.BIASED EXPONENT
The FPU represents exponents in a biased form. This means that a constant is added to the actual
exponent so that the biased exponent is always a positive number. The value of the biasing
constant depends on the number of bits available for representing exponents in the floating-point
format being used. The biasing constant is chosen so that the smallest normalized number can
be reciprocated without overflow.
(Refer to Section 7.4.1., Real Numbers for a list of the biasing constants that the FPU uses for
the various sizes of real data-types.)
7.2.3.Real Number and Non-number Encodings
A variety of real numbers and special values can be encoded in the FPUs floating-point format.
These numbers and values are generally divided into the following classes:
Signed zeros.
Denormalized finite numbers.
Normalized finite numbers.
Signed infinities.
NaNs.
Indefinite numbers.
(The term NaN stands for Not a Number.)
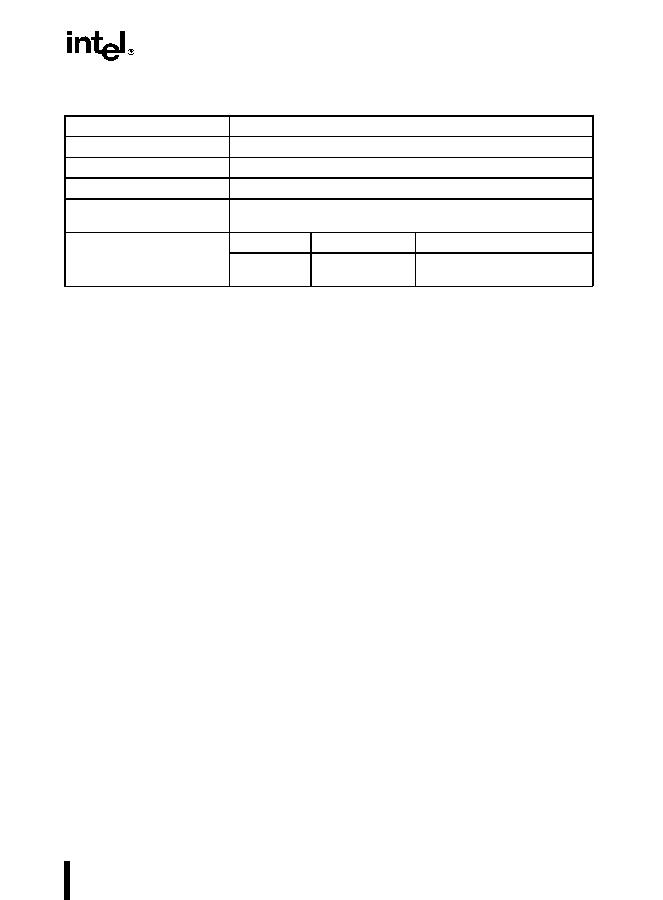
Table 7-1. Real Number Notation
Notation
Value
Ordinary Decimal
178.125
Scientific Decimal
1
.
78125E
10
2
Scientific Binary
1
.
0110010001E
2
111
Scientific Binary
(Biased Exponent)
1
.
0110010001E
2
10000110
Single-Real Format
Sign
Biased ExponentNormalized Significand
0
10000110
01100100010000000000000
1. (Implied)