7-7
FLOATING-POINT UNIT
When real numbers become very close to zero, the normalized-number format can no longer be
used to represent the numbers. This is because the range of the exponent is not large enough to
compensate for shifting the binary point to the right to eliminate leading zeros.
When the biased exponent is zero, smaller numbers can only be represented by making the
integer bit (and perhaps other leading bits) of the significand zero. The numbers in this range are
called denormalized (or tiny) numbers. The use of leading zeros with denormalized numbers
allows smaller numbers to be represented. However, this denormalization causes a loss of preci-
sion (the number of significant bits in the fraction is reduced by the leading zeros).
When performing normalized floating-point computations, an FPU normally operates on
normalized numbers and produces normalized numbers as results. Denormalized numbers
represent an underflow condition.
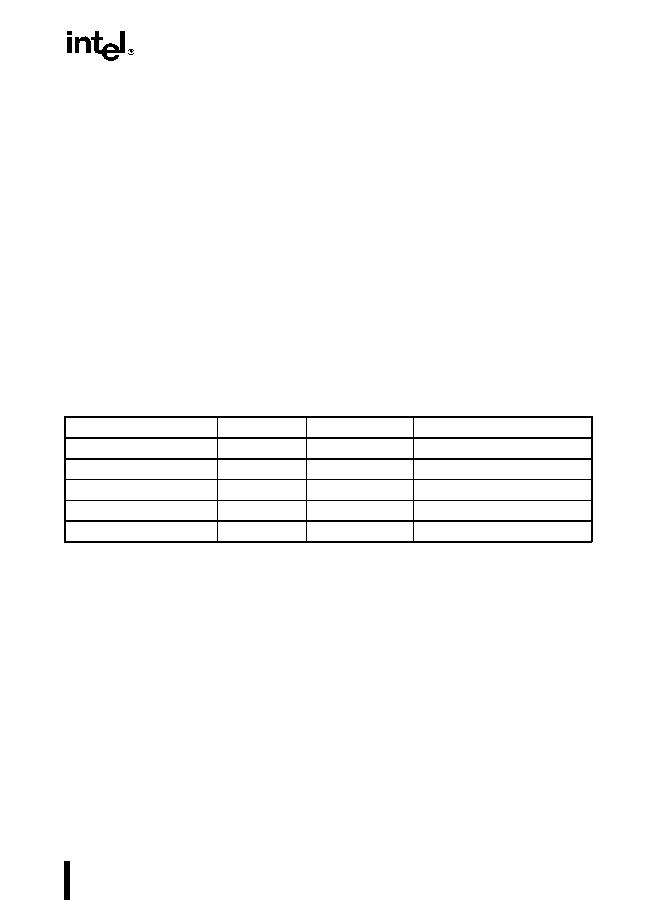
A denormalized number is computed through a technique called gradual underflow. Table 7-2
gives an example of gradual underflow in the denormalization process. Here the single-real
format is being used, so the minimum exponent (unbiased) is
?
126
10
. The true result in this
example requires an exponent of
?
129
10
in order to have a normalized number. Since
?
129
10
is beyond the allowable exponent range, the result is denormalized by inserting leading zeros
until the minimum exponent of
?
126
10
is reached.
NOTE:
* Expressed as an unbiased, decimal number.
In the extreme case, all the significant bits are shifted out to the right by leading zeros, creating
a zero result.
The FPU deals with denormal values in the following ways:
It avoids creating denormals by normalizing numbers whenever possible.
It provides the floating-point underflow exception to permit programmers to detect cases
when denormals are created.
It provides the floating-point denormal operand exception to permit procedures or
programs to detect when denormals are being used as source operands for computations.
When a denormal number in single- or double-real format is used as a source operand and the
denormal exception is masked, the FPU automatically normalizes the number when it is
converted to extended-real format.
Table 7-2. Denormalization Process
Operation
Sign
Exponent*
Significand
True Result
0
?
129
1.01011100000...00
Denormalize
0
?
128
0.10101110000...00
Denormalize
0
?
127
0.01010111000...00
Denormalize
0
?
126
0.00101011100...00
Denormal Result
0
?
126
0.00101011100...00